Linear grammar

In computer science, a grammar is linear if it is context-free and all of its productions' right hand sides have at most one nonterminal.

A linear language is a language generated by some linear grammar.

1 Example
2 Relationship with regular grammars
3 Expressive power
4 Closure properties
5 Notes
6 References

Example

A simple linear grammar is G with N = {S}, Σ = {a, b}, P with start symbol S and rules

S → aSb

S → ε

It generates the language 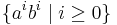$\{ a^ib^i \; | \; i \geq 0\}$ .

Relationship with regular grammars

Two special types of linear grammars are the following:

the left-linear or left regular grammars, in which all nonterminals in right hand sides are at the left ends;
the right-linear or right regular grammars, in which all nonterminals in right hand sides are at the right ends.

Collectively, these two special types of linear grammars are known as the regular grammars; both can describe exactly the regular languages.

Another special type of linear grammar is the following:

linear grammars in which all nonterminals in right hand sides are at the left or right ends, but not necessarily all at the same end.

By inserting new nonterminals, every linear grammar can be brought into this form without affecting the language generated. For instance, the rules of G above can be replaced with

S → aA

A → Sb

S → ε

Hence, linear grammars of this special form can generate all linear languages.

Expressive power

We have seen that all regular languages are linear; the example gave a linear, non-regular language. All linear languages are context-free by definition; a simple example of a context-free, non-linear language is the Dyck language of well-balanced bracket pairs.

Hence, the regular languages are a proper subset of the linear ones, which in turn are a proper subset of the context-free languages.

Closure properties

If L is a linear language and M is a regular language, then the intersection 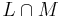$L \cap M$ is again a linear language; in other words, the linear languages are closed under intersection with regular sets. Furthermore, the linear languages are closed under homomorphism and inverse homomorphism^[1]. These three closure properties show that the linear languages form a full trio. Full trios in general are language families that enjoy a couple of other desirable mathematical properties.

Notes

^ see (Hopcroft & Ullman 1979), Ex. 11.1, pp. 282f.

References

John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-029880-X.